ATN
| BASIC keyword | |
| Keyword: | ATN |
| Abbreviation: | A Shift+T |
| Type: | Function |
| Token code: | 192/$C1 |
| Handling routine in BASIC ROM: |
58126–58234 $E30E–E37A |
| List of all BASIC keywords | |
Remark: This article describes the BASIC command ATN in BASIC V2 at the Commodore 64.
|
Type: Numeric Function |
The numerical function ATN is a mathematical function that returns the arc tangent of a numeric value (the inverse function of TAN). The resulting value is the angle in radians of the given tangent. To convert radians into degrees use the formula (rad*180/π) where rad is the angle in radians.
If the term given in the parentheses is non-numerical, the BASIC error ?TYPE MISMATCH ERROR occurrs. If the argument expression is not in the range of a floating point value the execution yields the BASIC error ?OVERFLOW ERROR. Omitting the numeric argument or to many arguments results in a ?SYNTAX ERROR.
Accuracy[edit | edit source]
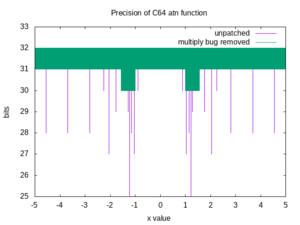
The graph to the right was obtained by comparing results from the BASIC ATN function to values computed on a modern x86-type PC.
At least for the plotted domain of [-5,+5], ATN matches the true value to 30 bits. No part of the domain proves to be problematic.
ATN calls POLY1, which calls MLTPLY ($BA59), and consequently the multiply bug affects its results. A small number of input values give results that match to only 25 bits.
Implementation details[edit | edit source]
Let the parameter be X.
The inverse tangent is an odd function; that is, ATN(-X) = -ATN(X). The BASIC routine uses this property to simplify its calculations a bit. It saves the sign, and then computes AX = |X|.
If AX > 1, ATN uses the identity ATN(X) = π/2 - ATN(1/X) to limit AX to the interval [0, 1].
It uses this polynomial approximation to calculate ATN(AX) for 0 <= AX <= 1:
- -6.8479391189*10-4 * T23 + 4.8509421558*10-3 * T21 - 1.6111701843*10-2 * T19 + 3.4209638048*10-2 * T17 - 5.4279132761*10-2 * T15 + 7.2457196540*10-2 * T13
- - 8.9802395378*10-2 * T11 + 0.11093241343 * T9 - 0.14283980767 * T7 + 0.19999912049 * T5 - 0.33333331568 * T3 + T
and modifies the result according to the identities described above.
The derivation of the polynomial is not publicly known.
Examples[edit | edit source]
PRINT ATN(1)
Output: 0.785398163
PRINT ATN(1)*4
Output: 3.1415266
The result is equivalent to π, but differs slightly from π caused by a wrong pressicion in the value of this constant
ABS | AND | ASC | ATN | CHR$ | CLOSE | CLR | CMD | CONT | COS | DATA | DEF | DIM | END | EXP | FN | FOR | FRE | GET | GET# | GOSUB | GOTO | IF | INPUT | INPUT# | INT | LEFT$ | LEN | LET | LIST | LOAD | LOG | MID$ | NEW | NEXT | NOT | ON | OPEN | OR | PEEK | π | POKE | POS | PRINT | PRINT# | READ | REM | RESTORE | RETURN | RIGHT$ | RND | RUN | SAVE | SGN | SIN | SPC | SQR | STATUS/ST | STEP | STOP | STR$ | SYS | TAB | TAN | THEN | TIME/TI | TIME$/TI$ | TO | USR | VAL | VERIFY | WAIT