SIN

BASIC keyword
Keyword:	SIN
Abbreviation:	S, Shift+I
Type:	Function
Token code:	191/$BF
Handling routine in BASIC ROM:	57963–58035 $E26B–E2B3
List of all BASIC keywords

Remark: This article describes the BASIC command SIN in BASIC V2 at the Commodore 64.

Type: Numeric Function General Programming-Syntax: SIN(<numeric-expression>)

The numeric function SIN is a mathematical function which evaluates to the sine for a given angle, a number regarded as being in radians.

If the term given in the parentheses is non-numerical, the BASIC error ?TYPE MISMATCH ERROR occurs. Being a floating point argument, the term must be in the range of ±2.93873588·10⁻³⁸ to ±1.70141183·10³⁸. Exceeding these limits yields the BASIC error ?OVERFLOW ERROR. Omitting the numeric argument or to many arguments results in a ?SYNTAX ERROR.

Implementation details

Error in various approximations of sin(2*π*x)

Let the parameter be X.

SIN first computes X2 = X/(2*π). It then computes I = INT(X2) and F = X2 - I, so that 0 <= F < 1. Because SIN is periodic, I is not needed after this point.

It then folds F into F2, such that |F2| <= 0.25 and SIN(F2*2*π) = SIN(F*2*π). The code is tricky to follow, but here is the final result:

• If 0 <= F <= 0.25, then F2 = F (quadrant I);
• If 0.25 < F <= 0.75, then F2 = 0.5 - F (quadrants II and III);
• If 0.75 < F < 1, then F2 = F - 1 (quadrant IV).

It finally computes SIN(X) using the following polynomial, which approximates SIN(F2*2*π) over [-0.25, +0.25]:

-14.381390672 * F2¹¹ + 42.007797122 * F2⁹ - 76.704170257 * F2⁷ + 81.605223686 * F2⁵ - 41.341702104 * F2³ + 6.2831853069 * F2

This polynomial is based of the taylor series of SIN , where x = 2*π*F2:

-x^11/11! + x^9/9! - x^7/7! + x^5/5! - x^3/3! + x

The Taylor series, however, requires eight terms to converge adequately within [-0.25,+0.25]. The polynomial in ROM accomplishes this feat with only six terms. Using fewer terms gives a faster function, especially given how slow floating point arithmetic is on a 6502.

Accuracy

Accuracy of SIN function

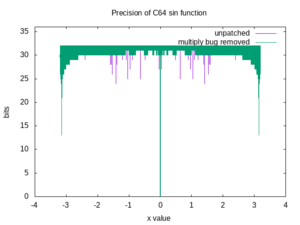
The graph to the right was obtained by comparing results from the BASIC SIN function to values computed on a modern x86-type PC.

Over most of the interval from about -2.6 to +2.6, SIN(x) matches the true value to 30 bits precision. This comes two bits short of the precision of the floating point type.

SIN calls POLY1, which calls MLTPLY ($BA59), and consequently the multiply bug affects its results. A small number of input values give results that match to only 24 bits.

Accuracy degrades somewhat for |x| greater than about 2.6. This happens because SIN(x) is calculated using the symmetry of the sin function, but the value of π used is not (and cannot be) exact.

Finally, accuracy becomes very poor for |x| less than about 0.05. This is because the polynomial coefficients are not (and cannot be) exact. Because sin(x) ≅ x for small x, the accuracy for this interval could be improved to about 24 bits by patching SIN to return its argument for |x| < 2^-11.

Examples

PRINT SIN(1)

Output: 0.841470985

Angles must be expressed in radians:

10 input "enter angle in radians";a
20 s=sin(a)
30 print "the sin of";a;"is";s

Run:

enter angle in radians? 1.57
the sin of 1.57 is .999999683

For angles expressed in degrees, the conversion must be done by hand:

10 input "enter angle in degrees";d
20 a=d*3.14159265359/180: s=sin(a)
30 print "the sin of";a;"is";s

Run:

enter angle in degrees? 90
the sin of 1.57079633 is 1

BASIC V2.0 (second release) Commands

ABS | AND | ASC | ATN | CHR$ | CLOSE | CLR | CMD | CONT | COS | DATA | DEF | DIM | END | EXP | FN | FOR | FRE | GET | GET# | GOSUB | GOTO | IF | INPUT | INPUT# | INT | LEFT$ | LEN | LET | LIST | LOAD | LOG | MID$ | NEW | NEXT | NOT | ON | OPEN | OR | PEEK | π | POKE | POS | PRINT | PRINT# | READ | REM | RESTORE | RETURN | RIGHT$ | RND | RUN | SAVE | SGN | SIN | SPC | SQR | STATUS/ST | STEP | STOP | STR$ | SYS | TAB | TAN | THEN | TIME/TI | TIME$/TI$ | TO | USR | VAL | VERIFY | WAIT