LOG

BASIC keyword
Keyword:	LOG
Abbreviation:	–
Type:	Function
Token code:	188/$BC
Handling routine in BASIC ROM:	47594–47655 $B9EA–BA27
List of all BASIC keywords

Remark: This article describes the BASIC command LOG in BASIC V2 at the Commodore 64.

Typ: Numeric Function 
General Programming-Syntax: LOG(<Numeric>)

The mathematical function LOG is a natural logarithm with the basis e(E). If the term is 0 or negative the BASIC error ?ILLEGAL QUANTITY ERROR IN line occurs. When the number is over 1.7014118342E+38 the BASIC-error ?OVERFLOW ERROR IN line appears. When the numeric argument is absent, a ?SYNTAX ERROR IN line appears.

Examples

PRINT LOG(1) Result: 0
PRINT LOG(10) Result: 2.30258509
PRINT LOG(100)/LOG(10) Result: 2
                       because you can divide by LOG(10) and get a result with the base "10". 

Implementation

Let the parameter be X. The LOG function first separates the exponent of X from the significand. That is, it calculates two numbers, N and XF, such that:

X = 2^N * XF, N is an integer and 0.5 <= XF < 1.0

C programmers will recognize this separation as the frexp() function.

The natural logarithm is tricky to calculate accurately. The Taylor series converges too slowly to be useful. The BASIC implementation uses a faster approach. Given XF calculated above, it calculates:

T = 1.0 - sqrt(2.0) / (XF + sqrt(0.5))

It then applies the polynomial approximation:

0.43425594189 * T⁷ + 0.57658454124 * T⁵ + 0.96180075919 * T³ + 2.8853900731 * T - 0.5

The result of this approximation is log₂(XF).

The routine then adds N to that approximation, resulting in log₂(X). Finally, it multiplies by LOG(2), giving the final result of LOG(X).

The derivation of the polynomial is not publicly known.

Accuracy

Accuracy of LOG function

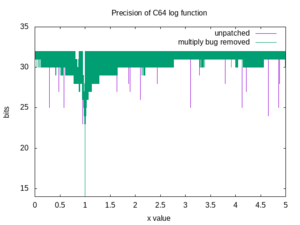
The graph to the right was obtained by comparing results from the BASIC LOG function to values computed on a modern x86-type PC.

At least for the plotted domain of (0,+5], LOG mostly matches the true value to 29 bits. Accuracy degrades around X equal to 1, where LOG(X) is close to 0. Better accuracy could be obtained by switching to the linear approximation log x = x-1 for x between 0.9 and 1.1.

LOG calls POLY1, which calls MLTPLY ($BA59), and consequently the multiply bug affects its results. A small number of input values give results that match to only 24 bits.

BASIC V2.0 (second release) Commands

ABS | AND | ASC | ATN | CHR$ | CLOSE | CLR | CMD | CONT | COS | DATA | DEF | DIM | END | EXP | FN | FOR | FRE | GET | GET# | GOSUB | GOTO | IF | INPUT | INPUT# | INT | LEFT$ | LEN | LET | LIST | LOAD | LOG | MID$ | NEW | NEXT | NOT | ON | OPEN | OR | PEEK | π | POKE | POS | PRINT | PRINT# | READ | REM | RESTORE | RETURN | RIGHT$ | RND | RUN | SAVE | SGN | SIN | SPC | SQR | STATUS/ST | STEP | STOP | STR$ | SYS | TAB | TAN | THEN | TIME/TI | TIME$/TI$ | TO | USR | VAL | VERIFY | WAIT