Pitfall
| Pitfall | ||
|---|---|---|
 | ||
| Game No. | 63 | |
| Voting | 6.39 points, 23 votes | |
| Developer | Peter Filiberti, David Crane | |
| Company | Activision | |
| Musician | Tim Shotter | |
| Release | 1983 | |
| Platform | Apple II, Atari 800, Atari VCS, C64, ColecoVision, MSX | |
| Genre | Platformer (Scrolling Screen) | |
| Gamemode | Single player | |
| Operation | ||
| Media | ||
| Language | ||
| Information | Follower: Pitfall II | |
Description[edit | edit source]
When David Crane's Pitfall! was released for the Atari VCS at the beginning of 1983, the game attracted the attention of the players not necessarily because of the great graphics (even though the graphics were probably above-average for this time and this console). In fact, Pitfall rose fast to the top of the game hit parades of that time due to its unique level buildup and its features and was because of its success converted to different other consoles and homecomputers (amongst them the C64) in the same year.
While most of the video games at that time only got harder or faster level by level and hardly offered any diversification in the course of the game, Pitfall had 255 different screens with a constant difficulty level, where enemies and perils alternated. There were further significant differences: e.g. when having contact with an enemy in Pitfall you "only" got points subtracted. But when this happend you could not reach the declared main aim, the maximum points, any more. Also you could not only - as usual - walk through the levels from left to right, the other direction was even easier!
Pitfall-Harry (the main character) had the possibility to switch betwen two different planes and survive his adventures there: the normal way on the surface or through an underground tunnel. The difference: if one used the underground way, then two screens were left out per screen change. So a treasure could easily be overlooked and again it would be over with the main aim (full points). There was also a time limit of exactly 20 minutes, which made it impossible to walk through all screens on the surface! Below the surface in return advancing was often averted by walls below the surface. So to get to all the hidden treasures you needed to choose the right combination of both ways.
Design[edit | edit source]
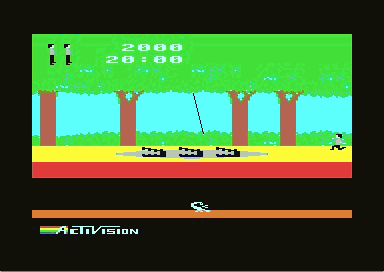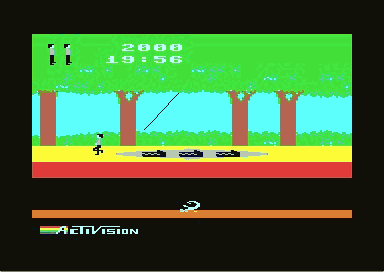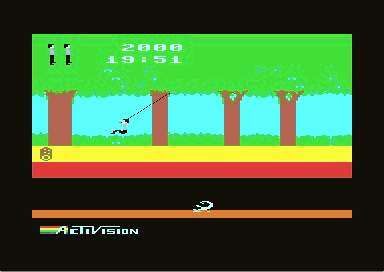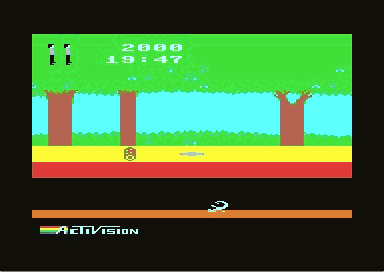 |
 |
At play, Pitfall was one of the best jump'n'run games of its time. You had to overcome pit traps and rolling logs with jumps, avoid enemies such as snakes and scorpions, and you could swing on lianas over quicksand or mud. But the player was never allowed to lose sight of the main aim, which was collecting the many different treasures. The graphics and sound did not use the full abilites of the C64 (no scrolling, switching of the screens, very rudimental fx), but one should not forget, that this was a very "early" game for the C64.
Hints[edit | edit source]
You start every game with 2000 points. If you fall into a hole, 100 points are subtracted. Rolling logs also reduce your points, the longer the contact with them is, the more points are subtracted.
If you find treasures, you get points. There are 8 different types of treasures in the game, altogether 32 treasures, which together have a value of 112.000 points. If you collect them all without losing points you can reach the perfect score of 112.000 + 2.000 = 114.000 !!
You have 20 minutes to finish the game. Pitfall Harry starts with 3 lives. The game ends when the time is over or Harry has lost all his lives.
Controls[edit | edit source]
![]() /
/ ![]() walk left / right
walk left / right
![]() /
/ ![]() jump left / right (also to jump on a liana and grab it)
jump left / right (also to jump on a liana and grab it)
![]() jump off a liana
jump off a liana
![]() /
/ ![]() climb ladder up / down
climb ladder up / down
![]() jump from crocodile to crocodile
jump from crocodile to crocodile
F1 to start the game
Run/Stop pause mode on (screen gets black); press again to go on playing
Run/Stop + Restore cancel game and start a new one
Points[edit | edit source]
- 2000 points Money Bag
- 3000 points Silver Bar
- 4000 points Gold Bar
- 5000 points Diamond Ring
Solution[edit | edit source]
Tips
- Developer David Crane himself hints to walk to the left right from the beginning. This makes playing easier, as especially the logs roll from right to left. Furthermore the character will be placed at the left border of the screen after losing a life, so that the corresponding screen can be run through more easily or you can start directly the following scene.
- To collect all 32 treasures you need to choose the correct route between underground and surface. At the surface the time limit is too short to get to the finish, in the underground the next screen is left out when leaving the current one, so a treasure can be easily missed out.
- To jump over crocodiles you need to bear in mind the following: wait until the mouth of the following crocodile is closed, then jump on its head, then wait until it opens and closes its mouth once before jumping to the next.
Cheats[edit | edit source]
- The "Remember" version offers different trainers.
Voting[edit | edit source]
| Voting of the C64-Wiki-User (10=the best vote): | ||
| 6.39 points at 23 votes (rank 727). You need to be logged in to cast a vote. | ||
| C64Games | 6 | 28th February 2009 - "good" 11086 downs |
| Lemon64 | 7,2 | 28th February 2009 - 38 votes |
| Kultboy.com | 7,65 | 26th June 2011 - 17 votes |
Reviews[edit | edit source]
Camailleon: "Somehow this doesn't seem to be my game, as I have the problem with this version to jump not precise enough. Maybe its just the practice missing. I got to know Pitfall on a PC - as Pifall II for Windows. The funny thing about it was, that the 8-bit version was integrated into it. Over a bonus level you got from the Windows 3D version into this one and you could spend the full 20 minutes or 3 lives in the 8-bit world."
Miscellaneous[edit | edit source]
- As in 1981 the first movie of the Indiana Jones series was published, David Crane could have been inspired by this concerning the plot of the game. On the other hand David Livingstone is also mentioned in the original manual...
Cover[edit | edit source]
 Front Cover |
 Back Cover |
Highscore[edit | edit source]

- PAT - 109.898 (11.05.2019)
- Werner - 71.752 (02.03.2009)
- Camailleon - 68.534 (05.12.2010)
- Blubarju - 66.274 (10.11.2010)
- Robotron2084 - 64.307 (15.10.2010)
Links[edit | edit source]
| Wikipedia: Pitfall! |
- C64Games.de - Game No. 133
- Lemon64 - Game No. 1943
- Gamebase64.com - Game No. 5731
- C64.com - Game No. 269
- Test Report No. 2467 on Kultboy.com




