COS (ROM Routine)
Note: This article describes the numeric COS routine in BASIC-ROM.
| Name: | COS | ||||||
| Description: | Calculate cosine of the floating point register FAC. | ||||||
| Entry point: | $E264 / 57956 | ||||||
| Passed arguments: | |||||||
| Return values: | |||||||
The ROM routine COS[1] — sometimes also as COSIN[2] - calculates the cosine of the angle. Its entry point is stored in the table of BASIC functions at address $A066, so that the routine is called by the BASIC interpreter each time the function COS is evaluated. The angle must be specified in Radians.
After the call, the value of the trigonometric function is in FAC, while the content of ARG is undefined. In addition to the contents of the floating-point registers FAC and ARG, COS also changes the auxiliary register at addresses 38/$26 to 41/$29, the floating-point register FAC#3 at addresses 87/$57 to 91/$5B and the trigonometric function sign flag at address 18/$12.
Algorithm[edit | edit source]
COS does not implement an independent calculation of the cosine, but only adds π/2 to the value stored in the floating point register FAC. The routine SIN that follows immediately in the ROM is then executed, which carries out the actual calculation. The ROM routine COS therefore uses the Identity cos(x) = sin(x + π/2).
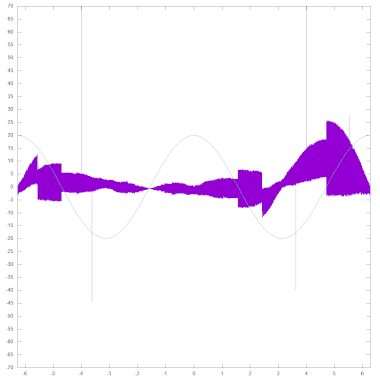
The graph below shows the deviation between the value returned by the COS routine and the exact cosine (purple, calculated as a double precision floating point number). For better orientation, the course of the cosine function is also shown (green, stretched by a factor of 20 in the y direction). To create the diagram, the values were not output with PRINT, but rather the binary content of FAC was read out before and after the COS routine was called. In this way, no inaccuracies or possible errors from the conversion from floating point representation to ASCII are included in the analysis. In addition, only the integer multiples of 2-15 in the interval ]-π/2; π/2[ is used to be able to look at exactly equidistant input values. The graph shows that the deviations between the result of COS and the exact cosine (from an average of 3.26E-10, a maximum of 25.75E-10, with individual outliers of up to 190.93E-10 due to an error in the multiplication routine) due to the additional calculation step in the derivation of SIN have increased significantly compared to the values there, and that sudden changes also occur at odd multiples of π/2.
Runtime behavior[edit | edit source]
The algorithm used by COS and the runtime behavior are documented in detail in the description of the ROM routine SIN. The only thing that needs to be added to the running times specified there is the calculation time for adding of π/2 to the FAC.
Bugs[edit | edit source]
- As can be seen from the above diagram showing the deviations between the result of COS and the exact cosine, the effects of a bug in FMULT are also reflected in the results of the ROM routine COS based on it: In total In 6 out of 411775 calculations of the analysis, this error caused a deviation of more than 30E-10, in the extreme case - when calculating COS(131449 / 32768) - even of 190.93E-10.
Links[edit | edit source]
- Disassembly of COS/$E264 on All About Your 64
- CodeBase 64: Floating Point Math
- C64 BASIC & KERNAL ROM Disassembly by Michael Steil
- C64OS: Floating Point Math from BASIC