ATN (ROM Routine)

Note: This article describes the numeric ATN routine in BASIC-ROM.

Name:			ATN
Description:			Calculate the arctangent of the floating point register FAC.
Entry point:			$E30E / 58126
Passed arguments:
Return values:

The ROM routine ATN — sometimes also as ARCTAN — calculates the Inverse Tangent of the number stored in the floating point register FAC. Its entry point is stored in the table of BASIC functions at address $A06C, so that the routine is called by the BASIC interpreter every time the function ATN is evaluated. The result is calculated in Radians.

After the call, the value of the ArcTangent is in FAC, while the content of ARG is undefined. In addition to the contents of the floating point registers FAC and ARG, ATN also changes the counter at address 103/$67, the auxiliary pointers at addresses 34/$22 (low byte) and 35/$23 (high byte) and 113/$71 (low byte). and 114/$72 (high byte) and the floating point registers FAC#3 and FAC#4 at addresses 87/$57 to 96/$60.

Algorithm

The ATN routine executes the following steps in sequence:

1. If the value in FAC is negative, the sign is reversed, but the original sign is always saved on the stack for later processing.
2. If the resulting value of FAC is greater than or equal to 1, it is replaced by its reciprocal; In the following, the ArcTangent is first calculated. The original exponent is also always saved to the stack.
   In all cases, FAC is now between 0 and 1.
3. FAC is now inserted into the following polynomial of 23rd degree, which is in the interval ' '[0; 1[ the function f(x) = atn(x) approximated. The associated Coefficients can be found in the ROM at address $E33E / 58158. To calculate the function value, the ROM routine POLY1 is called:
   p( x) = - 0.0006847939119 x23 + 0.004850942156 x21 - 0.01611170184 x19 + 0.03420963804 x17 - 0.054279132 76x 15 + 0.07245719654 x13 - 0.089802395 x11 + 0.1109324134 x9 - 0.1428398077 x7</ sup> + 0.1999991205 x5 - 0.3333333157 x3 + x
4. If it can be seen from the exponent buffered in the second step that the parameter passed to ATN was greater than or equal to 1 and was therefore calculated instead of the arctangent of the arctangent, this will now be the value of the corresponding arctangent determined by replacing the value p(x) in FAC with π/2 - p(x).
5. Finally, the sign of the original parameter secured in the first step is checked. If the parameter was negative, the value in FAC is now negated, since the arctangent function is point-symmetrical to the coordinate origin.

The following two diagrams show the graph of this polynomial (purple). In both images, the interval used by the ATN routine is colored light red. The course of the arctangent function (green) is also shown in the right image for comparison.

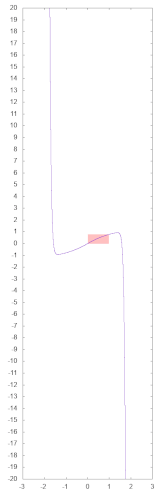
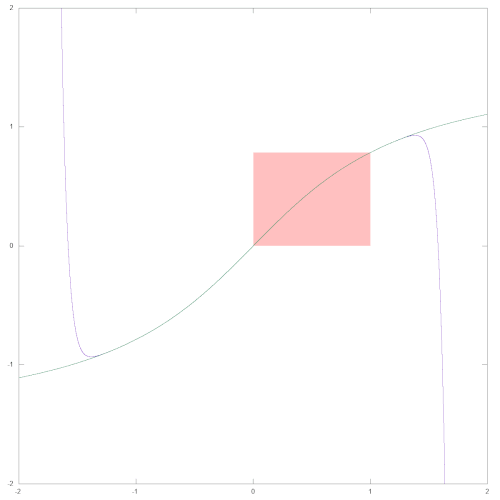
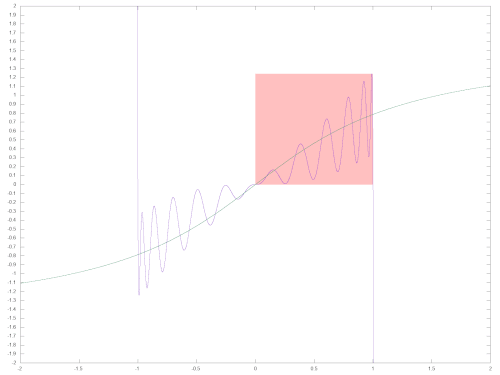
The next two pictures illustrate the quality of the approximation. The left image shows in the interval [-2, 2] the deviation between the approximation polynomial and the exact arctangent (purple), multiplied by 10¹⁰. These values were calculated as double-precision floating point numbers (52-bit Mantissa). The maximum Absolute Value] of the deviation determined in this way between p(x) and atn(x) is 1.24E-10 in the interval under consideration. For comparison, the arctangent function (green) is shown in the diagram.
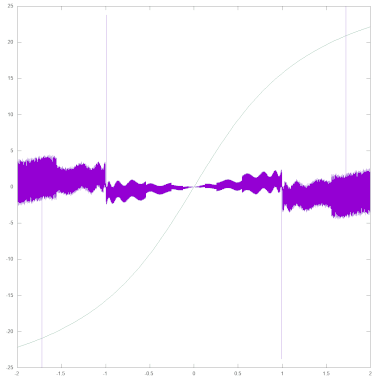
The right image shows the deviation between the value returned by the ATN routine and the exact arctangent (purple, again calculated as a double precision floating point number). For better orientation, the course of the arctangent function is also shown (green, stretched in the y-direction by a factor of 20). To create the diagram, the values were not output with PRINT, but rather the binary content of FAC was read out before and after the ATN routine was called. In this way, no inaccuracies or possible errors from the conversion from floating point representation to ASCII are included in the analysis. In addition, only the integer multiples of 2^-15 in the interval ]-2; 2[ used to be able to look at exactly equidistant input values. The diagram shows that the deviation between the approximation polynomial and the exact arctangent (of average 0.36E-10, maximum 1.24E-10) in the interval ]-1; 1[ is of a similar order of magnitude as the deviation between the result of the ATN routine and the arctangent (average 0.48E-10, maximum 2.39E-10). In the intervals [-2; -1] or [1; 2], in which the polynomial is applied to the reciprocal of the original parameter, on the other hand, differences between the results of the ATN routine and the arctangent (of 0.91E- on average) 10, maximum 4.45E-10, with individual outliers of up to 115.33E-10 clearly noticeable due to a error in the multiplication routine).

Runtime behavior

In each case, ATN evaluates the polynomial specified in step 3 of the algorithm. However, since the ROM routines FADD and FMULT used in POLY1 rely on a summand or a Factor from 0 and in this case do not carry out Addition or Multiplication, the call to ATN(0) only requires 4251 system clocks. In all other cases, due to the large number of arithmetic operations, a functional connection between the value transferred in FAC and the runtime of ATN cannot be recognized. In extensive series of measurements, the running time of ATN was between 34,847 and 43,439 system cycles.

On the Commodore 64, one system clock corresponds to around one microsecond (μs). In the worst case, the ATN routine requires a little more than 43 milliseconds (ms).

Bugs

• As can be seen from the diagram above with the deviations between the result of ATN and the exact arctangent, the effects of a bug in FMULT are also reflected in the results of the ROM routine ATN based on it: At total In 4 out of 131072 calculations of the analysis, this error caused a deviation of more than 10E-10, in the extreme case - when calculating ATN(56522 / 32768) - even of 115.33E-10.

Weblinks

• Disassembly of ATN/$E30E on All About Your 64
• CodeBase 64: Floating Point Math
• C64 BASIC & KERNAL ROM Disassembly by Michael Steil
• C64OS: Floating Point Math from BASIC