QINT

Note: This article describes the numeric QINT routine in BASIC-ROM.

Name:			QINT
Description:			Convert number in Floating point register FAC to 32-bit integer
Entry point:			$BC9B / 48283
Passed arguments:
Return values:

QINT - sometimes also referred to as FACINT - converts the content of the Floating point register FAC into a 32-bit integer, with all decimal places cut off and the value of the number rounded down to the next smaller integer if necessary. The number is stored in big-endian format, so that after the call the most significant byte is in the 1st mantissa byte at address 98/$62, the least significant byte is in the 4th mantissa byte at address 101/$65 stands. Negative integers are stored in the two's complement representation. The floating point number passed in FAC must be in the interval [ -2³¹-1; 2³¹-1 ] lie.

The ROM routine QINT only changes the contents of the floating point register FAC. It is the basis for the routines FACINX and INT and is also used in the BASIC ROM when setting the system time TI$, when outputting floating point numbers as a string and when processing memory addresses, i.e. called with the commands PEEK, POKE, SYS and WAIT.

Runtime behavior

QINT only checks for the special case FAC = 0 and returns the integer 0 after just 32 system cycles. All other floating point values are shifted to the right according to their exponent until the binary digit with the significance 2⁰ is in the least significant bit of the 4th mantissa byte. The shortest transit times therefore occur when the amount of FAC is in the interval [2³⁰, 2³¹-1] (93 cycles for positive, 186 cycles for negative numbers). The conversion of very small numbers takes the longest: For FAC = 2^-128, QINT delivers the result 0 ($00000000) after 7361 system cycles, for FAC = - 2^-128 only after 8244 cycles the result -1 ($FFFFFFFF).

The following diagram illustrates the computing time for converting a floating point number into an integer depending on the exponent (without excess). The green graph represents the running time for negative floating point numbers, the purple graph represents the running time for positive floating point numbers.

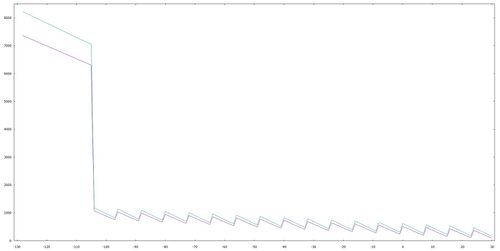
On the Commodore 64, one system clock corresponds to around one microsecond (μs). In the worst case, the QINT routine requires around 8 milliseconds (ms) for the conversion.

Bugs

• The number -2³¹ can also be represented as a 32-bit integer in two's complement. However, in this case, QINT shifts the mantissa of FAC one place to the right 256 times and finally delivers the incorrect result -1 ($FFFFFFFF) after a running time of 13166 system cycles.
• The test as to whether the mantissa of FAC should first be shifted to the right one byte at a time subtracts 160 (i.e. the excess plus the length of the mantissa) from the exponent and then examines the result:
  BCB1: CMP #$F9 ; Compare exponent-160 in A with the constant -7
BCB3: BPL $BCBB ; Branch for bitwise shifting if comparison result is positive
  If the original exponent including excess is now less than 24, then A has the value 120 or less - and the comparison command does not set the Negative flag , so that it is incorrectly shifted to the right not initially byte by byte, but only by bit, and the running time increases significantly. Correctly, after this comparison, you should instead branch with the Carry-Flag deleted. Even better would of course be an additional test to see whether the original exponent including excess is smaller than 129/$81 - in this case the value 0 can be returned directly for positive numbers and the value -1 for negative numbers .

Links

• Disassembly of QINT/$BC9B on All About Your 64
• CodeBase 64: Floating Point Math
• C64 BASIC & KERNAL ROM Disassembly by Michael Steil
• C64OS: Floating Point Math from BASIC