FOUT

Note: This article describes the numeric FOUT routine in BASIC-ROM.

Name:			FOUT
Description:			Convert number in Floating point register FAC to zero-terminated string
Entry point:			$BDDD / 48605
Passed arguments:
Other:			FAC = floating point number to be converted
Return values:
Accumulator:			0 = Low-Byte of the start address of the string
Y register:			1 = High-Byte of the start address of the string
Other:			Buffer from address 256/$0100 = Value of FAC as ASCII string

FOUT - sometimes also referred to as FLPSTR - converts the content of the floating point register FAC into a zero-terminated ASCII string starting at address 256/$0100. After the call, the content of FAC is undefined; a pointer to the resulting string is returned in the accumulator (Low-Byte) and in the Y-register (High-Byte).

In addition to the floating point register FAC and the string buffer from address 256/$0100, FOUT also changes the auxiliary buffers at addresses 71/$47, 93/$5D, 94/$5E and 113/$71.

Algorithm

1. First, FOUT checks the sign of FAC and, depending on this, stores a space (if FAC positive) or a minus sign (if FAC negative) as the first character of the string. The sign flag of FAC is then set to “positive”; All subsequent calculation steps are based on the amount of FAC.
2. If the value 0 is stored in FAC, this is recognized as a special case and only the number "0" is output directly.
3. Otherwise, FOUT brings the value of FAC into the interval [ 99999999.9; 999999999 ]. To do this, FAC is multiplied by 10 (using MUL10) or divided by 10 (using DIV10) until its value lies within this range. To save computing time, FOUT first checks whether the value of FAC is less than 1 - in this case at least a multiplication by 10⁹ = 1000000000 is required, and This can be done faster using FMULT than using nine consecutive calls to MUL10. The number of multiplications or divisions is recorded as a positive or negative value at address 93/$5D.
4. The number of multiplications or divisions is converted into a position for the decimal point (stored at address 93/$5D) and an exponent (at address 94/$5E). If the amount of FAC was originally smaller than 0.01 or larger or equal to 1E+09, this results in an exponent in the range -38...-3 (as two's complement) or in the range 9. ..38 and a decimal point after the first digit (position 1). Otherwise the exponent has the value 0 and the decimal point has a position between -1 (for example for the number 0.01) and 9 (for the number 100000000).
5. FAC is now converted to an integer in the interval [ 100000000; 999999999 ] converted. The values -100000000, 10000000, -1000000, 100000, -10000, 1000, -100, 10 and -1 are then added to this number one after the other until the sign changes due to the addition. The next digit to be output results from the number of additions required. If the position counter for the decimal point reaches the value 0 when counting down, the character "." issued
6. So that the string formed in this way does not end with the number "0" or with a decimal point, the string is now examined from the end for these characters and deleted if necessary. After deleting the decimal point or finding a digit other than "0", this cleanup is aborted.
7. If the exponent counter at address 94/$5E has the value 0, then no scientific notation is required and the conversion of FAC to a string is complete. Otherwise, FOUT outputs the character "E", the sign of the exponent and - always two digits - the exponent itself.

Runtime behavior

If the value 0 is transferred to the floating point battery FAC, FOUT recognizes this special case and only requires 61 system clocks. Otherwise, the computing time for the conversion is mainly determined by the number of multiplications by 10 or divisions by 10, the conversion to an integer and the repeated addition of positive and negative powers of ten. In extensive testing, the conversion took between 2136 cycles (for FAC = 190909090) and 88762 cycles (for FAC = 1.094909+38).

The left of the two following images shows the time for the conversion to a string when FAC is successively with all combinations of the digits 1, ..., 9 and the exponents E-37, ..., E +37 is loaded. Plotted on the abscissa axis is the sum exponent + (digit 1) / 9, so that the measured values are plotted equidistantly. It can be clearly seen that the running time increases for very small numbers (numerous calls to the ROM routine MUL10) and very large numbers (numerous calls to DIV10). Because DIV10 is significantly slower than MUL10, the longest running times occur when converting very large floating point numbers.

The diagram on the right illustrates the running time when converting the numbers 1, ..., 1000000 into strings. The abscissa for each number x is the value log₁₀(x)+1, roughly corresponding to the number of digits in x. In addition to the influence of the exponent, the interaction of the individual digits can also be seen in the running times plotted here. In this value range, the shortest running time is 3946 system cycles (for the number 190909), the longest is 7942 cycles (for the number 9). Contrary to obvious expectations, the single-digit numbers here are the ones that take the longest to convert into a string.

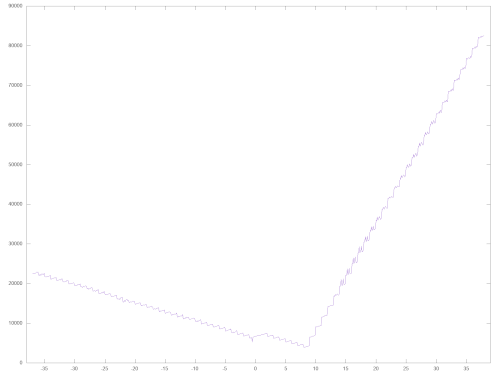
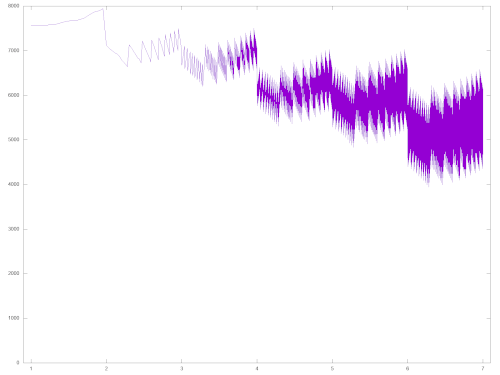
On the Commodore 64, one system clock corresponds to around one microsecond (μs). In the worst case, the FOUT routine requires around 89 milliseconds (ms) for the conversion.

Bugs

In the third step of the algorithm, the value of FAC is converted into the interval [ 99999999.90625; 999999999.25 ] brought. However, for a correct conversion the value must be at least 99999999.95, otherwise rounding errors may occur when converting to a string:

?99999999.9,99999999.91 99999999.9 100000000

Links

• Disassembly of FOUT/$BDDD on All About Your 64
• CodeBase 64: Floating Point Math
• C64 BASIC & KERNAL ROM Disassembly by Michael Steil
• C64OS: Floating Point Math from BASIC